10172. Vertex
Write a program that
searches a directed graph for vertices which are inaccessible from a given
starting vertex.
A directed graph is
represented by n vertices,
numbered consecutively 1, ..., n, and a series of
edges p → q which connect the pair
of nodes p and q in one direction
only.
A vertex r is reachable from a
vertex p if
there is an edge p → r, or if there exists some
vertex q for
which q is reachable
from p and r is reachable from q.
A vertex r is inaccessible from a
vertex p if r is not reachable from p.
Input. Consists of several
directed graphs and starting nodes. For each graph, there is first one line
containing a single integer n (1 ≤ n ≤ 100). This is the number
of vertices in the graph.
Following, there will be a
group of lines, each containing a set of integers. The group is terminated by a
line which contains only the integer 0. Each set represent a collection of
edges. The first integer in the set i is
the starting vertex, while the next group of integers j, ..., k, define the series
of edges i → j, ..., i → k, and the last
integer on the line is always 0. Each possible start
vertex i (1 ≤ i ≤ n) will appear once or not at all. Following each graph
definition, there will be one line containing a list of integers. The first
integer on the line will specify how many integers follow. Each of the
following integers represents a start vertex to be investigated by your
program. The next graph then follows. If there are no more graphs, the next
line will contain only the integer 0.
Output. For each start vertex to be
investigated, your program should identify all the vertices which are
inaccessible from the given start vertex. Each list should appear on one line,
beginning with the count of inaccessible vertices and followed by the
inaccessible vertex numbers.
|
Sample input |
Sample output |
|
3 1 2 0 2 2 0 3 1 2 0 0 2 1 2 0 |
2 1 3 2 1 3 |
SOLUTION
graphs – Floyd
- Warshall
Algorithm analysis
Construct the adjacency matrix of the graph c. Run the Floyd-Warshall algorithm to find all shortest paths in a graph. For vertex i, those vertices j for which c[i][j] = ¥, will be
unreachable after the Floyd – Warshall algorithm is executed. The complexity of the algorithm is O(n3).
Example
Consider the given sample.
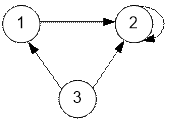
The example explores two vertices:
the first and the second. It is impossible to get to the first and the third vertices from the
first and the second one.
Algorithm realization
The input graph is stored in an
adjacency matrix with size MAX = 101.
#define MAX 101
int c[MAX][MAX];
Floyd – Warshall algorithm
implementation.
void floyd(void)
{
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if (c[i][k]
+ c[k][j] < c[i][j])
c[i][j] = c[i][k] +
c[k][j];
}
The main part of the program. Read the graph and build an
adjacency matrix c. Initially, set
all edges to be equal to infinity (we’ll choose the hexadecimal value
3F3F3F3F as infinity). Since the
vertices of the graph are numbered from one by the problem statement, the zero
row and column of the matrix c will not be used.
while(scanf("%d",&n),
n > 0)
{
memset(c,0x3F,sizeof(c));
while(scanf("%d",&a) ,a)
while(scanf("%d", &b), b) c[a][b] = 1;
Run the Floyd-Warshall algorithm on the adjacency
matrix c.
floyd();
Read the number of vertices i under investigation for a given graph, and for each investigated vertex a, count the number of vertices b unreachable from a (for which c[a][b] = ¥).
scanf("%d",&i);
while(i--)
{
scanf("%d",&a);
Count the number of vertices
unreachable from a.
for(count =
0, b = 1; b <= n; b++)
if
(c[a][b] == 0x3F3F3F3F) count++;
Print the number of
unreachable vertices from a and the
vertices themselves in ascending order of numbers.
printf("%d",count);
for(b = 1;
b <= n; b++)
if (c[a][b] == 0x3F3F3F3F) printf(" %d",b);
printf("\n");
}
}
Java
realization
import java.util.*;
public class Main
{
static int c[][];
static int n;
static void floyd()
{
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if (c[i][k] + c[k][j] < c[i][j])
c[i][j] = c[i][k] + c[k][j];
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(true)
{
n = con.nextInt();
if (n == 0) break;
c = new int[n+1][n+1];
for(int i = 0; i <= n; i++)
Arrays.fill(c[i],Integer.MAX_VALUE / 2);
while(true)
{
int a = con.nextInt();
if (a == 0) break;
while(true)
{
int b = con.nextInt();
if (b == 0) break;
c[a][b] = 1;
}
}
floyd();
int i = con.nextInt();
while(i-- > 0)
{
int a = con.nextInt();
int count = 0;
for(int b = 1; b <= n; b++)
if (c[a][b] == Integer.MAX_VALUE / 2) count++;
System.out.print(count);
for(int b = 1; b <= n; b++)
if (c[a][b] == Integer.MAX_VALUE / 2) System.out.print(" " + b);
System.out.println();
}
}
con.close();
}
}